2021 Kolokwium 2
Zadanie 1
Dla \(n \geq 4\) znajdź liczbę etykietowanych drzew \(n\)-wierzchołkowych, w których \(\{ 1,2,3 \}\) jest zbiorem niezależnym.
Wskazówka: Udowodnij, że liczba drzew \(n\)-wierzchołkowych, które zawierają
drzewo 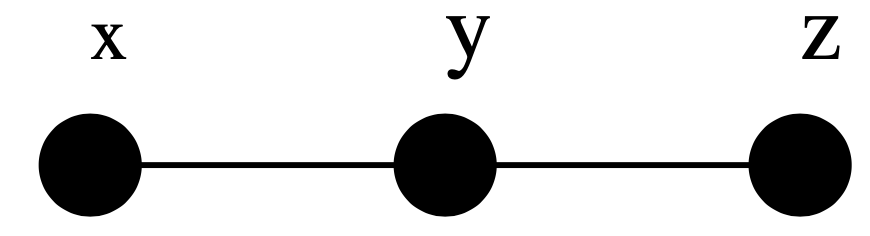 jako podgraf, jest równa \(3n^{n-4}\).
jako podgraf, jest równa \(3n^{n-4}\).
Zadanie 2
Znajdź wielomian chromatyczny grafu.
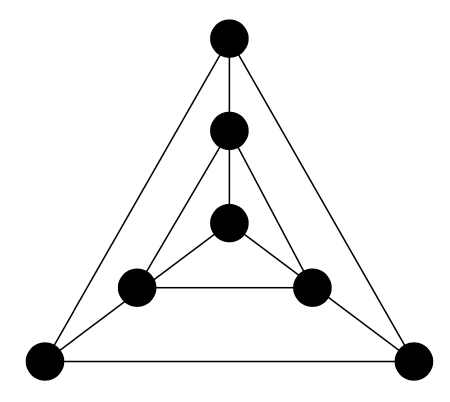
Zadanie 3
Niech \(p,q,r>2\) będą różnymi liczbami pierwszymi. Udowodnij, że:
\[
\forall x\quad x^{(pqr-pq-pr-qr+p+q+r+3)/4}\equiv x\pmod{pqr}
\]